Python: Sets¶

I set (insiemi) sono una collezione non ordinata di elementi senza ripetizioni.

Per definire un insieme, posso scrivere:

sette_nani = {"Brontolo", "Pisolo", "Dotto", ...}

I set possono essere visti come dizionari di sole chiavi.

La sintassi e’:

{ valore1, valore2, ...}

Posso creare un set vuoto utilizzando la funzione set:

empty_set = set()
print(type(empty_set))            # set
print(len(empty_set))             # 0

empty_set2 = {}
print(type(empty_set2))           # dict

La stessa funzione puo’ essere utilizzata per creare un set a partire da una lista:

set_numeri = set([1, 2, 3])
print(set_numeri)                 # {1, 2, 3}

I set possono essere utilizzati per rimuovere le ripetizioni da una lista::: lista = [0, 1, 0, 0, 2, 0] insieme = set(lista) print(insieme) # {0, 1, 2}

Operazioni¶

Ritorna	Operatore	Significato
`int`	`len(set)`	Restituisce il numero di elementi nel set
`bool`	`object in set`	Controlla se l’elemento e’ presente nel set
`None`	`set.add(object)`	Inserisce un elemento
`None`	`set.update(list)`	Inserisce una lista di elementi
`None`	`set.remove(object)`	Rimuove un elemento (errore se non presente)
`None`	`set.discard(object)`	Rimuove un elemento

Esempio. Partendo da un set vuoto:

numeri_fortunati = set()

print(numeri_fortunati)              # set()
print(len(numeri_fortunati))         # 0

inserisco i primi cinque numeri naturali:

primi_cinque = range(5)
numeri_fortunati.update(primi_cinque)
print(len(numeri_fortunati))         # 5

inserisco i numeri pari tra 0 e 10 (incluso):

pari = [x for x in range(11) if x % 2 == 0]
numeri_fortunati.update(pari)
print(len(numeri_fortunati))         # 8

provo a rimuovere "0":

numeri_fortunati.discard("0")        # non fa nulla
numeri_fortunati.remove("0")         # errore

aggiungo la stringa "0" al set e controllo che sia presente:

numeri_fortunati.add("0")
"0" in numeri_fortunati              # True

Warning

Come per i dizionari, c’e’ alcuna garanzia che un set preservi l’ordine in cui vengono inseriti gli elementi.

Warning

I set sono oggetti mutabili, come nel caso delle liste conviene prestare attenzione per evitare situazioni spiacevoli, ad esempio:

pasto_completo = {'antipasto', 'primo', 'secondo', 'dolce', "caffe'"}

pasto_ridotto = pasto_completo
pasto_ridotto.remove('antipasto', 'dolce')

print(pasto_completo)
{'primo', 'secondo', "caffe'"}    # Doh!

Per creare una copia di un set:

L = {1, 2, 3}
copia_di_L = set(L)
copia_di_L.remove(2)
print(copia_di_L)                 # {1, 3}
print(L)                          # {1, 2, 3}

PROVATE VOI Esercizi

Creare:
1. Un set vuoto set_vuoto. Controllare che sia vuoto con len().
2. Un set primi10 contenente i primi 10 numeri naturali. Controllare se contiene 10, in caso contrario, inserirlo e ricontrollare che sia presente. Rimuoverlo nuovamente.
3. Un set primi10no7 contenente i primi 10 numeri naturali, tranne 7 (partendo da primi10 ma lasciandolo inalterato). Controllo che 7 sia presente in primi10 e assente in primi10no7.
4. Ricreare primi10no7, questa volta utilizzando una list comprehension.

Operazioni¶

Ritorna	Operatore	Significato
`set`	`set.union(set)`	Restituisce l’unione di due set
`set`	`set.intersection(set)`	Restituisce l’intersezione tra due set
`set`	`set.difference(set)`	Restituisce la differenza tra due set

Esempio. Creo il set dei primi dieci numeri naturali:

set_A = set(range(10))

Creo il set dei multipli di 3 compresi tra 0 e 20:

set_B = set([x for x in range(20) if x % 3 == 0])

Creo l’unione di set_A e set_B:

unione = set_A.union(set_B)
print(unione)                             # {0, 1, 2, 3, .., 8, 9, 12, 15, 18}

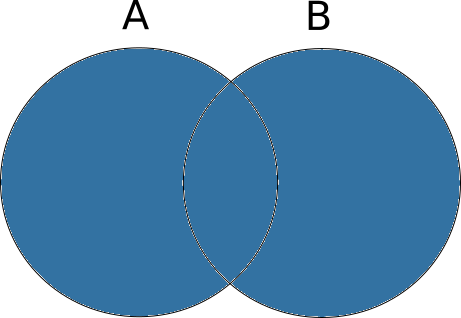
Ora creo l’intersezione di set_A e set_B:

intersezione = set_A.intersection(set_B)
print(intersezione)                       # {0, 3, 6, 9}

Nota: le operazioni di unione e intersezione sono simmetriche, per qualsiasi set_A e set_B vale:

set_A.union(set_B) == set_B.union(set_A)                 # True
set_A.intersection(set_B) == set_B.intersection(set_A)   # True

Ottengo i numeri naturali tra 0 e 9 che NON sono multipli di 3:

diff1 = set_A.difference(set_B)
print(diff1)                              # {1, 2, 4, 5, 7, 8}

Analogamente, ottengo i multipli di 3 fino al 18 che NON sono compresi tra 0 e 9:

diff2 = set_B.difference(set_A)
print(diff2)                              # {12, 15, 18}

Nota al contrario di unione ed intersezione, la differenza non e’ simmetrica!

Esercizi¶

Per ogni testo, creare l’insieme delle parole che contiene (maiuscole/minuscole non contano):
```
testo_A = "Le due ore di informatica piu' noiose della vostra vita"
testo_B = "La vita e' come una scatola di cioccolatini"
testo_C = "Cioccolatini come se piovesse LA La lA laaa"
```
1. Contare il numero di parole diverse per ognuno dei tre testi.
2. Ottenere gli insiemi delle parole in comune tra i tre testi: condivise_A_B, condivise_A_C, condivise_B_C.
3. Dati i set creati precedentemente, ottenere l’insieme delle parole che compaiono in almeno due testi, utilizzando soltanto operazioni tra set.
4. Ottenere l’insieme delle parole che compaiono esattamente in un testo. Hint posso farlo utililizzando il risultato precedente?
5. Ottenere l’insieme delle parole che compaiono ripetute nello stesso testo.

Soluzioni¶

Soluzioni:

Soluzione:

set_vuoto = {}
print(set_vuoto)
print(len(set_vuoto))                        # 0

Soluzione:

primi10 = set(range(10))
print(10 in primi10)                         # False
primi10.add(10)
print(10 in primi10)                         # True
primi10.remove(10)

Soluzione, provo cosi’:

primi10no7 = primi10
primi10no7.remove(7)
print(7 in primi10)                          # False

Ricordo che i set sono strutture mutabili:

primi10 = set(range(10))                     # Ricreo il set originale
primi10no7 = set(primi10)
primi10no7.remove(7)
print(7 in primi10)                          # True
print(7 in primi10no7)                       # False

Soluzione:

primi10no7 = set([x in range(10) if x != 7])
print(primi10no7)                            # Controllo

Soluzione:

Convertendo i testi in minuscolo:

tA_lower = testo_A.lower()
tB_lower = testo_B.lower()
tC_lower = testo_C.lower()

Creo gli insiemi delle parole contenute nei testi:

parole_in_A = set(tA_lower.split())
parole_in_B = set(tB_lower.split())
parole_in_C = set(tC_lower.split())

Conto per ogni testo il numero di parole diverse:

len(parole_in_A)                             # 10
len(parole_in_B)                             # 8
len(parole_in_C)                             # 6

Ottengo le parole in comune utilizzando l’intersezione:

condivise_A_B = parole_in_A.intersection(parole_in_B)
condivise_A_C = parole_in_A.intersection(parole_in_C)
condivise_B_C = parole_in_B.intersection(parole_in_C)

Controllo:

print(condivise_A_B)           # {'vita', 'di'}
print(condivise_A_C)           # set()
print(condivise_B_C)           # {'la', 'cioccolatini', 'come'}

Soluzione:

almeno_in_2 = condivise_A_B.union(condivise_A_C).union(condivise_B_C)
print(almeno_in_2)             # {'vita', 'di', 'la', 'cioccolatini', 'come'}

Creo l’insieme di tutte le parole contenute nei tre testi:

tutte_le_parole = parole_in_A.union(parole_in_B).union(parole_in_C)

Ottengo le parole che appaiono esattamente in **UN* testo:

solo_in_uno = tutte_le_parole.difference(almeno_in_2)
print(solo_in_uno)
{'le', 'una', 'se', 'vostra', 'della', 'laaa', "piu'", 'ore', "e'", \
'piovesse', 'scatola', 'noiose', 'informatica', 'due'}

Ci sono diversi modi per farlo. Una soluzione (consideriamo solo testo_A per brevita’):

ripetute_in_A = set([p for p in parole_in_A \
                     if tA_lower.count(p) > 1])